8.2 Riconoscimento della LIN con errore quadratico medio minore

Questa tecnica ha la stessa funzione della struttura K-LIN: serve per riconoscere il parlatore, al fine di poter utilizzare il suo modello per il riconoscimento delle successive frasi pronunciate da quel parlatore. Può quindi essere collocata tra le tecniche di categorizzazione del parlatore.

È stata descritta in questa tesi, poichè la teoria su cui basa il suo funzionamento ha dimostrato di essere corretta. Questa tecnica ha diversi pregi. Purtroppo l'incapacità di compiere un passaggio, cioè l'inversione della rete neurale, l'ha resa inapplicabile. Con future ricerche si potrebbero, però, trovare dei metodi che compiono questo passaggio in modo approssimato, permettendone la completa applicabilità. Per modellare le caratteristiche fonetiche dei parlatori si utilizzano anche in questo caso delle LIN.

Una LIN effettua una trasformazione lineare sui paramentri di ingresso al fine di renderli il più possibile simili agli ingressi che si aspetterebbe la rete SI per quel determinato fonema. Nel caso venga utilizzata una LIN appartenente ad un parlatore con caratteristiche vocali differenti rispetto a quello giusto, la trasformazione sugli ingressi compiuta dalla LIN, sarà peggiore rispetto all'utilizzo diretto dei pattern di ingresso.

Se è possibile ottenere gli ingressi ottimali, per un determinato target, da fornire alla rete al fine di ottenere il target, si può pensare di fare un confronto tra gli ingressi ottimi e gli ingressi trasformati dalle varie LIN. La LIN che fornirà l'uscita maggiormente simile all'ingresso ottimo della rete, sarà la LIN rappresentativa del parlatore, che verrà scelta per i successivi riconoscimenti.

Come criterio di similitudine si è scelto l'errore quadratico medio tra le 273 uscite di ogni LIN e i 273 ingressi ottimali per la rete SI. Tale scelta, a seguito di una verifica compiuta più avanti in questo capitolo, è risultata ragionevole.

Le LIN devono essere addestrate in modo robusto, con materiale proveniente dallo stesso parlatore. Nei nostri esperimenti si sono addestrate 4 LIN, una per ognuno dei parlatori del database italiano DB-Micro, con 285 frasi e 5 epoche. Si partirà a spiegare questa tecnica nell'ipotesi che sia possibile ottenere gli ingressi ottimi riferiti ad un pattern per la rete SI, successivamente in questo capitolo verrà trattato il problema di come ottenerli. Con lo stesso pattern utilizzato per ricavare gli ingressi ottimi, si può effettuare il run-forward delle LIN riferite ai parlatori, ottenendo una serie di ingressi trasformati dalle LIN (figura 8.2).

Tra gli ingressi trasformati, quelli riferiti alla LIN del parlatore e alle LIN dei parlatori con caratteristiche vocali simili, saranno più simili agli ingressi ottimi, rispetto agli altri. Sia $o_i = (o_1,o_2,...,o_{273})$ l'input ottimo e sia $o_i^p = (o_1^p,o_2^p,...,o_{273}^p)$ l'output ottenuto dal run-forward della LIN riferita al parlatore $p$, l'errore quadratico medio sarà:

$$E^p = \sum_{i=1}^{273} \left( o_i - o_i^p \right)^2$$ (8.4)

Una volta calcolati gli errori quadratici medi per ogni parlatore attraverso la formula (8.4), la LIN con errore quadratico medio minore sarà quella rappresentativa del parlatore.

Figure 8.2: Schema del riconoscimento della LIN con errore quadratico medio minore

Come accennato in precedenza, l'aspetto più difficile di questa tecnica consiste nel trovare gli input ottimi per un determinato pattern. Utilizzando la rete neurale per un normale riconoscimento, con il principio utilizzato nell'addestramento non supervisionato si riesce a ricavare un target. Target con una precisione che oscilla dal 70% all'80%. Un errore del 30% sulla creazione del target fornisce una precisione sufficiente per ottenere dati significativi nella scelta del modello. Il riconoscitore, in ogni caso, fornisce lo score una misura di confidence: quanto è probabile che ciò che è stato riconosciuto sia veritiero. Analizzando solo i pattern con confidence più alta si può abbattere notevolmente l'imprecisione nella creazione dei target.

Una volta ottenuto il target, si possono cercare gli ingressi ottimi per ottenere quel target. Una prima soluzione è stata quella di cercare un metodo che permettesse di invertire l'intera rete neurale. Si è riscontrato che la rete neurale non è invertibile per i seguenti motivi:

• sapendo l'output di un nodo, ci sono infiniti possibili ingressi che possono averlo generato
• la funzione sigmoide, di generazione degli output dei nodi della rete neurale, è invertibile. Purtroppo, il programma di addestramento NNA compie un troncamento a 6 cifre decimali. Ci possono perciò essere infiniti ingressi che danno, come uscita della funzione sigmoide, il valore 1
• la funzione softmax, presente nell'ultimo strato della rete neurale, non è invertibile

Per risolvere il problema si sono cercati dei metodi approssimati. Utilizzando l'algoritmo di back propagation per addestrare una rete, l'unico parametro che è possibile regolare è il learning rate $\eta$. Per la LIN di ogni parlatore si è trovato il valore di learning rate $\eta$, che minimizza l'errore quadratico medio. Una volta trovato il learning rate ottimo per tutte le LIN, quella con errore quadratico medio minore sarà la vincente. Sia $o_i = (o_1,o_2,..,0_{273})$ l'input ottimo per la rete SI, sia $o_i^p = (o_1^p,o_2^p,..,o_{273}^p)$ l'output della LIN riferita al parlatore $p$ e sia $i_i = (i_1,i_2,...,i_{273})$ il pattern di ingresso, l'errore quadratico medio potrà essere scritto nel seguente modo:

$$E = \sum_{i=1}^{273} \left( o_i^p - i_i - o_i + i_i \right)^2 \mbox { \ \ \ dove}$$ (8.5)

$$\Delta o_i = o_i - i_i = \sum_{j=1}^{273}\left( \eta \cdot \... ... \cdot \sum_{j=1}^{273}\left( \Delta w_{ij} \cdot i_j \right)$$ (8.6)

In formula (8.6) si sono potute utilizzare le variazione dei pesi, anziché il valore esatto, poiché la trasformazione compiuta da LIN è una trasformazione lineare. Sostituendo l'equazione (8.6) in (8.5) si può scrivere l'errore come:

$$E = \sum_{i=1}^{273}\left( \Delta o_i^p - \eta \cdot \sum_{j=1}^{273} \left( \Delta w_{ij} \cdot i_j \right) \right)^2$$ (8.7)

Poichè l'equazione (8.7) ha un minimo, si può trovare il valore di $\eta$ per cui la derivata parziale del primo ordine dell'equazione, rispetto ad $\eta$, valga 0:

$$\frac{\partial E}{\partial \eta} = \sum_{i=1}^{273} \left( -... ... \Delta w_{ij} \cdot i_j \right) \right) \right) = 0 \nonumber$$

$$\eta = \frac{\sum_{i=1}^{273} \left( \sum_{j=1}^{273}\left( ... ...m_{j=1}^{273} \left( \Delta w_{ij} \cdot i_j \right) \right) }$$ (8.8)

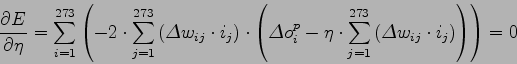Per i calcoli è stata fatta la semplificazione che la LIN sia interamente interconnessa. Nel nostro caso le LIN utilizzate sono connesse a blocchi: $\sum_{j=1}^{273}$ di formula (8.9) deve essere divisa in 7 sommatorie da 39 elementi, che variano i loro estremi in dipendenza del valore di $i$. Una volta trovati i learning rate ottimi per ogni LIN, si possono inserire nell'equazione (8.7) per trovare l'errore quadratico medio associato ad ogni LIN, ed ottenere la rete con errore minimo.

A seguito dell'implementazione pratica dell'architettura descritta, si è potuto constatare che il metodo di determinazione degli ingressi ottimi non riesce a fornire, con sufficiente precisione, gli ingressi al fine di ottenere il target desiderato. I parlatori vengono riconosciuti in modo quasi casuale. L'algoritmo di back propagation tende, infatti, a minimizzare il gradiente dell'errore rispetto al target, compiuto durante il riconoscimento. Non è un metodo esatto, esso abbassa l'errore ad ogni pattern, minimizzandolo progressivamente. Anche andando a cercare il valore di $\eta$ ottimo, l'algoritmo non è sufficientemente preciso per fornire, con un solo pattern di ingresso, un valore accurato. Purtroppo in questa tecnica, rimane aperto il problema di come trovare l'ingresso ottimale per un determinato target.

Essa è stata descritta in questa tesi per l'indubbio vantaggio di essere molto veloce:

• con pochi patterns si riesce a riconoscere l'identità del parlatore. Mandando in ingresso a tutte le LIN lo stesso pattern e cercando l'ingresso ottimo per un determinato target, viene infatti svincolata la dipendenza dal pattern nella scelta del parlatore
• come per la tecnica K-LIN, viene fatto un unico run-forward della rete SI