Subsections
2.2.2 Addestramento
Il processo di training di una rete neurale consiste nell'addestrare i suoi pesi ed i suoi bias attraverso l'utilizzo di esempi detti patterns. Senza questa fase, la rete non potrebbe mai essere utilizzata per il riconoscimento. A tale scopo esistono degli algoritmi di cui, il più importante e quello utilizzato in questo lavoro è l'algoritmo di back-propagation.
Esistono due tipi possibili di training:
- supervised learning (addestramento supervisionato)
- unsupervised learning (addestramento non supervisionato)
2.2.2.1 Supervised learning
In questo tipo di training si danno in input alla rete dei patterns con associato la classe di appartenenza (traget) nota a priori. In questo schema, dando in input un determinato pattern, ottengo un risultato. Tale risultato viene elaborato mediane back-propagation in modo da apportare una correzione dei pesi e dei bias al fine di rendere minimo tale errore (figura 2.4).
2.2.2.2 Unsupervised learning
Un addestramento di tipo unsupervised viene invece utilizzato tutte le volte in cui, per quelche motivo, non si ha a disposizione il target. Questo metodo ha risultati peggiori rispetto a quello supervised ma ha due particolari pregi: può essere utilizzato in modo real time, cioè durante il normale funzionamento della rete in riconoscimento, e permette di addestrare la rete senza nessun intervento umano. Nel metodo supervised, infatti, c'è bisogno di un intervento esterno per dare al target il giusto valore e per consentire l'apprendimento del pattern. Tale intervento può essere in alcune situazioni fastidioso per l'utente il quale, ogni qualvolta che la rete sbaglia, deve correggerla manualmente fornendone il valore esatto.
Figure 2.4:
Processo di supervised lerning
|
|
Il funzionamento è abbastanza intuitivo, anche se presuppone la presenza di una rete già semi-addestrata, che mi possa cioè dare un riconoscimento accettabile. Questa è una grossa limitazione del metodo, perché ne vede impossibile l'utilizzo nelle prime fase di addestramento. In pratica, quando arriva un nuovo pattern da addestrare se ne fa un riconoscimento. Il valore ottenuto sarà preso come target: verrà messo a 1 il risultato con probabilità maggiore e a 0 tutti gli altri. A questo punto si può procedere ad un addestramento di tipo supervised. Ovviamente il target non sarà sempre corretto e, in quei casi, si opererà un addestramento sbagliato alla rete, le cui prestazioni tenderanno a peggiorare. Nella media, però, si avranno molti target corretti e la rete tenderà naturalmente ad evolvere verso uno stadio di ottimo, anche se in modo meno preciso e più lento rispetto all'addestramento supervised.
Anche se è un'espressione un po' forte, c'è da ipotizzare che la rete tenda a migliorare quei risultati per cui da già valori di riconoscimento validi, aumentando in ogni caso la qualità della rete, ma raggiungendo un limite molto lontano da quello che potrebbe ottenere andando a correggere anche dove sbaglia sempre. Non è comunque da escludere che il miglioramento generale della qualità, possa portare a correggere anche casi dove prima sbagliava sempre.
2.2.2.3 Back-propagation
L'algoritmo di back-propagation venne proposto nel 1986 da Rumelhart. Esso ha lo scopo di addestrare una rete neurale di tipo multi-layer perceptron. In questa sezione daremo una descrizione dettagliata di tale algoritmo, perché costituisce il nucleo di funzionamento di una rete neurale.
L'algoritmo della back-propagation usa il criterio della discesa del gradiente per minimizzare l'errore quadratico medio tra gli output desiderati e quelli ottenuti.
Figure 2.5:
Diminuzione dell'errore quadratico medio nella back-propagation
|
|
Sia 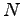 il numero di output della rete, si definisce
il numero di output della rete, si definisce
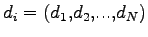 il vettore degli output desiderati riferito al pattern
il vettore degli output desiderati riferito al pattern 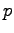 e
e
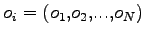 il vettore degli output ottenuti attraverso la rete neurale al pattern
il vettore degli output ottenuti attraverso la rete neurale al pattern 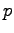 .
Con queste ipotesi, l'errore quadratico medio è dato dalla seguente funzione:
.
Con queste ipotesi, l'errore quadratico medio è dato dalla seguente funzione:
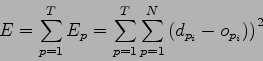 |
(2.5) |
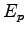 rappresenta l'errore compiuto per il riconoscimento del pattern
rappresenta l'errore compiuto per il riconoscimento del pattern 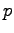 Il vettore
Il vettore 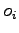 è funzione puramente dei pesi
è funzione puramente dei pesi 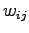 della rete, così anche la funzione di errore
della rete, così anche la funzione di errore 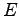 . Il problema dunque consiste nel minimizzare una funzione di
. Il problema dunque consiste nel minimizzare una funzione di 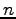 variabili dove
variabili dove 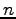 rappresenta il numero di pesi della rete. Solitamente le reti neurali hanno un numero elevato di pesi, dovuto alla presenza di diversi livelli di rete, di solito completamente interconnessi. Tale circostanza obbliga l'utilizzo della tecnica di discesa del gradiente attraverso la minimizzazione delle derivate parziali (figura 2.5).
rappresenta il numero di pesi della rete. Solitamente le reti neurali hanno un numero elevato di pesi, dovuto alla presenza di diversi livelli di rete, di solito completamente interconnessi. Tale circostanza obbliga l'utilizzo della tecnica di discesa del gradiente attraverso la minimizzazione delle derivate parziali (figura 2.5).
Quindi, preso un qualsiasi livello 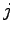 della rete si ha che i pesi vengono modificati attraverso la funzione:
della rete si ha che i pesi vengono modificati attraverso la funzione:
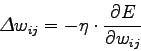 |
(2.6) |
dove 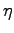 rappresenta il learning rate, cioè il fattore di apprendimento della rete. Solo con un'accurata scelta del learning rate si riesce ad ottenere un giusto compromesso tra l'apprendimento di nuovi patterns senza dimenticare i patterns visti in precedenza.
rappresenta il learning rate, cioè il fattore di apprendimento della rete. Solo con un'accurata scelta del learning rate si riesce ad ottenere un giusto compromesso tra l'apprendimento di nuovi patterns senza dimenticare i patterns visti in precedenza.
Figure 2.6:
Grandezze di riferimento utilizzate per spiegare l'algoritmo di back-propagation
|
|
Nella realtà la funzione di correzione degli errori (2.6) si complica leggermente per l'aggiunta di un fattore, il momento, che ha lo scopo di evitare che i pesi oscillino, durante l'addestramento, attorno ad un valore medio senza dare nessun miglioramento. In pratica il momento costringe i pesi della rete a spostarsi verso la direzione dello spostamento dei pesi al frame precedente. La (2.6) si può perciò scrivere come:
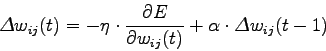 |
(2.7) |
in cui 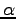 è il momento e
è il momento e 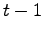 rappresenta il frame antecedente al frame
rappresenta il frame antecedente al frame 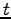 . Durante il seguito dei calcoli si utilizzerà l'espressione (2.6), poichè il momento, essendo solo dipendente da dati calcolati al tempo
. Durante il seguito dei calcoli si utilizzerà l'espressione (2.6), poichè il momento, essendo solo dipendente da dati calcolati al tempo 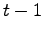 , può essere aggiunto a
, può essere aggiunto a 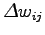 come ulteriore fattore della somma.
Con riferimento a figura (2.6), limitandoci ad analizzare due livelli della rete
come ulteriore fattore della somma.
Con riferimento a figura (2.6), limitandoci ad analizzare due livelli della rete 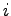 e
e 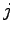 , riscriviamo le funzioni che regolano la rete neurale in accordo con le nuove variabili:
, riscriviamo le funzioni che regolano la rete neurale in accordo con le nuove variabili:
Per la determinazione della variazione dei pesi 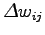 si può procedere dalla (2.7) nel modo seguente:
si può procedere dalla (2.7) nel modo seguente:
La derivata parziale dell'equazione (2.10) si può ottenere dalla (2.9),
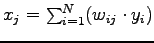 , ottenendo:
, ottenendo:
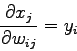 |
(2.12) |
Per risolvere la seconda derivata parziale dell'equazione (2.11) si fa ricorso all'inversa dell'equazione (2.8) trovando:
Per risolvere invece la prima derivata parziale, occorre dividere tale soluzione in due parti: soluzione del livello di output della rete e soluzione dei livelli sottostanti.
Affrontiamo quindi il primo punto, in cui
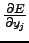 rappresenta l'errore tra il pattern riconosciuto e il target:
rappresenta l'errore tra il pattern riconosciuto e il target:
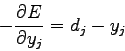 |
(2.14) |
A seguito dei risultati ottenuti, l'equazione (2.11) potrà essere scritta, sfruttando (2.13) e (2.14) come:
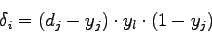 |
(2.15) |
Si ricorda che tale equazione ha una sua logica solo per il livello di output della rete neurale e che l'algoritmo di back-propagation funziona partendo dal livello di output, scendendo ai livelli inferiori della rete, fino ad arrivare al livello di input.
Per un livello generico della rete si prosegue in modo pressochè simile partendo dalla scomposizione della prima derivata della formula (2.11):
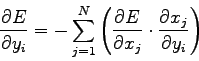 |
(2.16) |
I due termini di si (2.16) possono ottenere rispettivamente dalla (2.11) e dalla derivata parziale dell'equazione di attivazione (2.9) rispetto 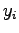 trovando:
trovando:
Sostituendo (2.17) e (2.18) in (2.16) e poi il risultato in (2.11) si ottiene per un generico livello:
![\begin{displaymath}
\delta_i = \left[ \sum_{j=1}^{N} \left( \delta_j \cdot w_{ij} \right) \right] \cdot y_j \cdot \left( 1-y_j \right)
\end{displaymath}](img64.png) |
(2.19) |
A questo punto è possibile calcolare per le unità di ogni livello la variazione da fornire al peso della connessione con i nodi del livello successivo. E' da notare che per risolvere il livello 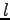 è necessario aver risolto il livello
è necessario aver risolto il livello 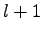 , si dovrà perciò partire dal livello di output per arrivare ad aggiornare i pesi fino al livello di input.
Conoscendo le formule che regolano la convergenza ed il funzionamento dell'algoritmo di back-propagation, possiamo scriverne in modo completo i passi:
Stefano Scanzio
2007-10-16
, si dovrà perciò partire dal livello di output per arrivare ad aggiornare i pesi fino al livello di input.
Conoscendo le formule che regolano la convergenza ed il funzionamento dell'algoritmo di back-propagation, possiamo scriverne in modo completo i passi:
Stefano Scanzio
2007-10-16
![]() della rete si ha che i pesi vengono modificati attraverso la funzione:
della rete si ha che i pesi vengono modificati attraverso la funzione:
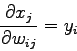
![\begin{displaymath}
\delta_i = \left[ \sum_{j=1}^{N} \left( \delta_j \cdot w_{ij} \right) \right] \cdot y_j \cdot \left( 1-y_j \right)
\end{displaymath}](img64.png)
![$\displaystyle \left[ \sum_{j=1}^{N} \left( \delta_j \cdot w_{ij} \right) \right] \cdot y_j \cdot \left( 1-y_j \right) \mbox{ per le unit\\lq a interne}$](img73.png)